ここをクリックすると、項目ページに戻ります。
***************************************************
　 h13.01.04
＝＝＝「コンピュータが展開図を作成するために必要な情報(1)」＝＝＝
コンピュータが、何らかの構造情報を入力され、それをもとに展開図を描くとすれば
そのとき用いることのできるアルゴリズムとして今の時点で現実的なものとして
円領域分子法があげられる。ここでコンピュータが円領域分子法を実行するには
どのような情報があればよいかを検討してみよう。例えば図１のような基本枝構造に
対応する展開図を描くことを考えよう。

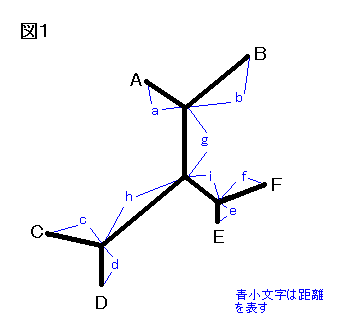
このときコンピュータが直接扱う情報の量はどのくらいになるだろうか。
基本的には折ろうとする全てのカドの組み合わせを考えて、各組み合わせの２つの
カドの間の距離を扱えばよいのである。すなわち、折ろうとするカドの数がＮ個だとすると、

　　コンピュータが展開図を描くために扱う距離情報の数　＝　Ｎ　かける　（Ｎ−１）　わる　２

となる。例えば６個のカドを折り出す展開図をコンピュータが描こうとするならば、

　　コンピュータが展開図を描くために扱う距離情報の数　＝　６　かける　５　わる　２　＝　１５
　
というわけで、１５個の距離情報を扱えばよいのである。この辺の話はLang氏の
プログラムTreeMakerのマニュアルにも同様のことが書かれているので参照されたい。
この距離情報をどのように扱うのかというと、極めて単純で、要するに、各カドの
組み合わせに応じた距離（これは展開図上では各カドに対応する円領域の中心点間の
距離のことである）には、これ以上接近してはいけないという限界があるので（表１参照のこと）、

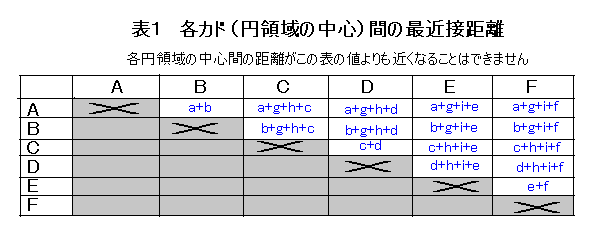
この限界以上接近しないように距離をモニターしながら、適当に展開図を作っていく
というふうに距離情報を利用すればよいのである。
なぜ各カドの組み合わせに応じてこれ以上は接近できないような距離があるのかというと、
これまた単純な話で、円領域が重なってはいけないという条件を単純に距離を含む式で
表しただけのことである。
ところで、ここで強調しておきたいことがある。それは、人間が円領域分子法を
考えるときには円とか帯とかといった図形パターンを認識しているので、コンピュータ
にも同じようなパターン認識をさせなくてはいけないのではないだろうか、などど
真面目な人は考えてしまうかもしれないが、実はコンピュータに円領域分子法を
実行させる場合は、円とか帯とかといった図形のパターン認識をさせる必要はない
のである。おおまかに言ってしまうと、コンピュータは距離だけ扱っていれば、
結果的に人間が円とか帯とかといったパターン認識をした場合と同様の結果を導き出せる
のである（もちろん巧拙の差はあるが）。


さて、実際は今述べた距離の取り扱いだけでは、円領域分子法のうち
円領域的な面しか考慮していない。次回は、距離情報をもとに円領域分子法の分子的な面を扱うにはどうするかを述べてみたい。

ここをクリックすると、ページ戻ります。