ここをクリックすると、項目ページに戻ります。
***************************************************
　 h13.01.06
＝＝＝「コンピュータが展開図を作成するために必要な情報(2)」＝＝＝
先日アップした「コンピュータが展開図を作成するために必要な情報(1)」の中で
円領域分子法をコンピュータが実行するために必要な情報は、非常に単純化すると
距離情報だけでよくって、「展開図上での円領域の中心間の距離には、これ以上
接近してはいけないという限界（これを今後最近接可能距離と呼ぼう）があること
を利用する」としたが、これでは円領域分子法のうち、円領域的な扱いだけに注目
していることになってしまう。円領域分子法と言うからには、分子的な扱いは
どうするかという事も同時に考えなくては片手落ちである。
では分子をコンピュータが扱うためにはどのような情報が必要だろうか。
真面目に考える人は、「分子の扱いというのは典型的なパターン認識で、それを
コンピュータに扱わせるのは大変だろう」などど考えてしまうかもしれないが、
例によって実際は全然大変ではない。ではどうすれば良いかというと、一値分子の
境界線上で隣接している２つの円領域の中心間の距離を、最近接可能距離と同じにすれば
よいだけである。この様子を図１に示したのでご覧いただきたい。

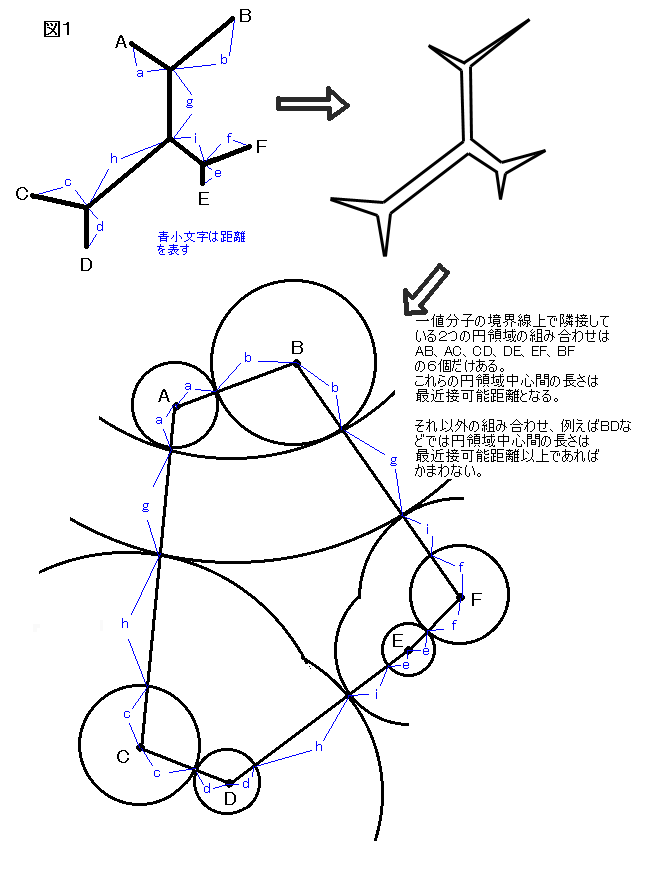
さて、以上のことをふまえると「コンピュータに円領域分子法を実行させる場合は、
コンピュータは円領域の中心間の距離を扱えばよい」といったが、実はこの扱い方
は円領域の組み合わせに応じて２つの場合があるということに気が付く。

（１）一値分子の境界線上で隣接している２つの円領域の組み合わせを考える場合
　　円領域の中心間の距離　＝　最近接可能距離
（２）上記の（１）以外の場合
　　円領域の中心間の距離　＞＝　最近接可能距離
（注、＞＝　という記号は見慣れない人もいるかもしれないが、この意味は
ただ単に、「円領域の中心間の距離は最近接可能距離以上である」といっている
だけである。）
（注、ちなみに　＜＝　という記号は「以下」を表す）　

このことを表１にまとめたので参照されたい。

　　　
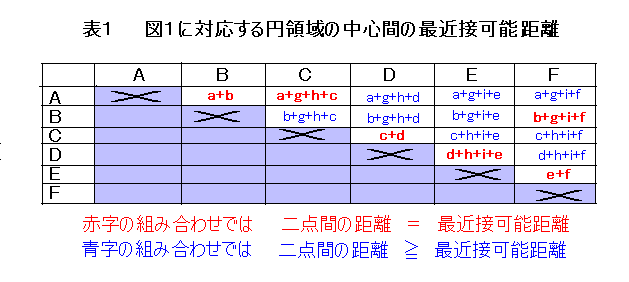
さて、実際には今述べた距離情報だけで細かい設計をするのは難しいので更なる工夫が
必要になる。次回からは、距離情報の式に、各種の情報を扱える式を評価関数として
加えていくことを試みることにする。

ここをクリックすると、ページ戻ります。