ここをクリックすると、項目ページに戻ります。
***************************************************
　 h13.01.10
＝＝＝「簡単な評価関数を定義する」＝＝＝
これまでコンピュータが展開図を作成するために必要な情報を簡単に見てきたが
それらをもとに評価関数を実際に立ててみよう。
しかし、ここでやはり問題があって、それは別のところに書いたことの繰り返しになるのだが
おりおでは「全体の評価関数の値が大きい方が望ましい」と定義したので、自然科学一般の
最適化問題に見られる「関数値がより小さいものを解として求める」という傾向と
逆になっている。人間の感覚で評価関数を論じるときはおりおのやり方で問題ないのだが、
コンピュータで与えられた条件のもとでの最適解としての展開図を求めようとするときは
「関数値がより小さいものを解として求める」方式にしないと、他の自然科学分野との
連携が不自然になって、困ってしまうのだ。そこで、コンピュータが展開図を求めるときは
展開図の位置エネルギー（E）を定義して、位置エネルギーが低いほうが望ましい展開図
ということにする。そうすると評価関数（Ｈ）と位置エネルギーの関係は
　　　Ｈ＝　−Ｅ　＋　α　　　　　　（式１）
であらわされる。これならＥの値が低いほどＨの値が高くなって定義に良く合う。

ではＥの内容について見てみよう。くどくなるが、Ｅの値が小さいほど望ましい展開図で
あるということを忘れないでほしい。
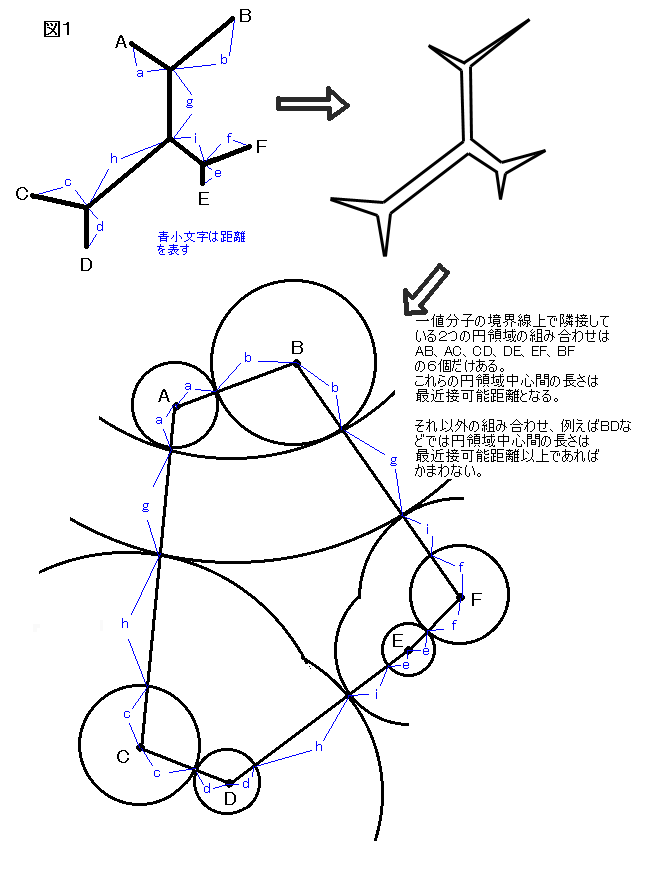
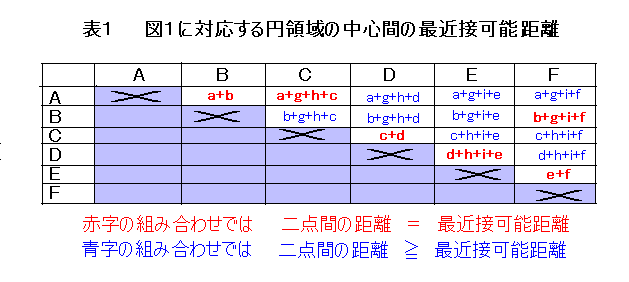
これまで用いてきた例を今回も使おう。図１の形と表１の最近接可能距離を再確認してほしい。


とりあえず、Ｅを構成する項について箇条書きしてみる。
（１）Ｅ距離　円領域中心間の距離に関するエネルギー
（２）Ｅ場所　円領域が用紙の内部にあるか辺縁部にあるかに関するエネルギー
（３）Ｅ効率　用紙の使用効率に関するエネルギー
（４）Ｅ紙形　用紙の形が正方形か別の形かに関するエネルギー

とりあえずこんなところを扱ってみよう。
上記の（１）から（４）までを考慮すると、全体の位置エネルギーＥは

　　Ｅ ＝ ｋ距＊Ｅ距離 ＋ ｋ場＊Ｅ場所 ＋ ｋ効＊Ｅ効率 ＋ ｋ紙＊Ｅ紙形　　（式２）

といった形であらわせるだろう。ここで＊は　かけ算　の意味である。
ｋ距、ｋ場、ｋ効、ｋ紙、はそれぞれ対応するエネルギーの重みを表す。
例えば、用紙使用効率が重要だと考えるならばｋ効の値を大きくすればよい。
さて、よく考えるとＥが式２で本当に表せるという保証はどこにもない、っていうか、
本当はこんな単純な式であらわせる訳がないのだが、最初から話を複雑にしても
しょうがないので当面は式２の形を使っていこう。これでも近似式としてはまあまあで、
現行の折紙設計プログラムよりは進化した形になっているはずである（多分）。
では各項の実際の計算式を見ていこう。
まず　Ｅ距離 であるが、距離情報として扱うべきものは、前にも書いたが、
ＡＢの距離、ＡＣの距離、ＡＤの距離、ＡＥの距離、ＡＦの距離、ＢＣの距離、
ＢＤの距離、ＢＥの距離、ＢＦの距離、ＣＤの距離、ＣＥの距離、ＣＦの距離、
ＤＥの距離、ＤＦの距離、ＥＦの距離、という１５通りの点の組み合わせに関するもの
である。このうちＡＢ、ＡＣ、ＣＤ、ＤＥ、ＥＦ、ＢＦ、については、その実際の展開図上
での距離が、対応する最近接可能距離と等しいときに、最も望ましく（つまりエネルギー最小）
なるように式をたてればよい。これも、いろいろな工夫ができるところだが、
最も簡単なものは各組み合わせごとに下式の値を計算して合計することである。
なお、下式では例として組み合わせＡＢについて書いているが、他の組み合わせの
計算式も全く同様である。
ＡＢの距離に関するエネルギーを　Ｅab、
ＡＢの展開図上での実際の距離を　Ｌab、
ＡＢの最近接可能距離を　Ｌabmin、とすると

　　Ｅab　＝　ｋ＊（Ｌab−Ｌabmin）＊（Ｌab−Ｌabmin）

ここでｋは各組み合わせごとの重みをあらわす適当な係数である。

また、ＡＤ、ＡＥ、ＡＦ、ＢＣ、ＢＤ、ＢＥ、ＣＥ、ＣＦ、ＤＦ、については、
その実際の展開図上での距離が、対応する最近接可能距離以上であれば同じように
望ましいわけだから、例として組み合わせＡＤについて書いてみると、

　ＬadがＬadminより小さいときは 　　Ｅad　＝　ｋ＊（Ｌad−Ｌadmin）＊（Ｌad−Ｌadmin）

　ＬadがＬadmin以上のときは 　　Ｅad　＝　０

としよう。
以上を総合して考えると、Ｅ距離の値は以下のようになる。

　Ｅ距離＝　Ｅab＋Ｅac＋Ｅcd＋Ｅde＋Ｅef＋Ｅbf＋
　　　　　　Ｅad＋Ｅae＋Ｅaf＋Ｅbc＋Ｅbd＋Ｅbe＋Ｅce＋Ｅcf＋Ｅdf　

　 さて、よく考えるとＥ距離も本当は上式のように表せるという保証はどこにもないが
ようするに、近似式としてこんな感じのはずということである。


こんどは円領域が用紙の内部にあるか辺縁部にあるかに関するエネルギーであるＥ場所について
考てみたい。
それには用紙をどういう風に表すかを考えなくてはいけない。できるだけ簡単な
定義のほうが良いので
　-a ＜＝ x ＜＝ a
　-b ＜＝ y ＜＝ b
を満たす四角形で用紙を表すことにしよう。ここで、aとbは変数であることに
注意しておいてほしい。
すると、例えば円領域Ｄの中心のｘ座標とｙ座標をＤx、Ｄy　とし、
点Ｄ（辺在性の点とします）に関する場所のエネルギー値を　Ｅ場所(D)　とすると、これは例えば以下のような関数で表せる。

　Ｅ場所(D)＝min（abs（Ｄx＊Ｄx−a＊a）　,　abs（Ｄy＊Ｄy−b*b）　）

ここでmin（α,β）はαとβの小さいほう値をとるという関数である。
また、abs（γ）は、γの絶対値の意味である。
この式は実際に図にしてみるとは非常に簡単な形で、用紙の境界線の上だけが零で、
それ以外は何らかの正の値をとる関数である。

こんどは、用紙の使用効率に関するエネルギー（Ｅ効率）について考えてみよう。
単純に用紙の使用効率が高ければ高いほど良い展開図と仮定するなら、例えばであるが　

　Ｅ効率＝　a＊a＋b＊b

といった式で一応簡単に表すことができる。

最後に用紙の形が正方形か別の形かに関するエネルギー（Ｅ紙形）　は今回は
正方形を優先するという評価関数を考えることにしたいので、一例として
　　Ｅ紙形＝（a-b）＊（a-b）

と書くこともできるであろう。

以上でだいたい評価関数の実際の形をとりあえず定義したことになる。
ただし、この評価関数は、多くの創作者が重要視する原子の角度等の考慮が
なされておらず、不満を感じる人も多いと思う。ただ、原子の角度の扱いは、面倒なので
とりあえずは、今定義した評価関数を実際にプログラム化することを行ってみたい。
　
ここをクリックすると、ページ戻ります。