ここをクリックすると、メインページに戻ります。
===============================================================================
===============================================================================
=====第１０話　クモ類の設計======
クモ類を折り紙で折ることは、かなり困難なことでした。
今でも、設計的な技術を用いないとしたら、スマートなクモを不切正方形一枚から折ることは
とても困難です。
しかし、最近クモを折る技術が急速に開発されました。
この結果、事情を知る折り手にとって、クモの折り紙は、すでに各種の特徴の折分けを追求できる
ような融通のきくものとなりつつあります。
（当ページでは目黒や、S太郎氏、みるかし姫氏の作品を掲載させていただいていますので
合わせて参照して下さい。）
ここでクモの折紙の設計法についてまとめて、どなたでも気楽にクモの設計ができるように
解説してみたいと思います。
使っている技法は折り紙にたいする情熱が少しでもあれば、必ず理解、実行できますので、
興味のある方は難しそうだなどと考える前に、まずはお試しくださいませ。

前置きが長くなりましたが、早速実行に入りたいと思います。
大まかな設計手順としては特にクモだからといって他のテーマと異なる必要はありません。
円領域分子法のオーソドックスな方法で行ってみましょう。

手順１
設計をはじめる前に自分の折りたいクモの形をよく観察したり、まとめておいたりしましょう。
具体的には、どの足がどのくらいの長さで胴体がどのくらいの長さか、蝕肢はどうするか、
などの方針をまとめておきましょう。

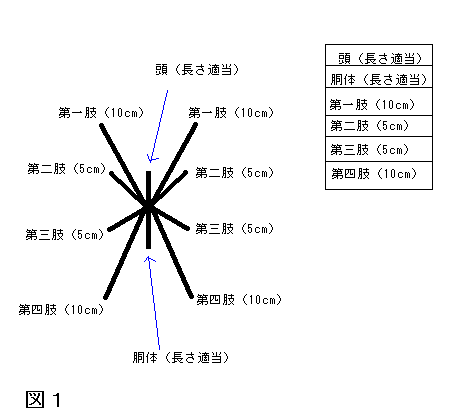
ここでは、前から１対目の足10cm、２対目の足5cm、３対目の足5cm、
４対目の足10cm、蝕肢は無し（0cm）頭、胴体の長さは適宜決める
という方針でいきましょう。
このとき図１のような樹状図を描きながら各パーツの長さを決めるのは
とても有効です。




手順２
さてさて、折りたいパーツの長さが決まったら、次にやることは円図の作成です。
円図の作成では、折り出したいカドを円で表して、
それを用紙上に配置します。
設計になれていない人は、「円図とはいったいこ何だろう？」と、
不思議に思うかもしれません。しかし、心配はご無用です。
円図とは極めて簡単なものなので、多分、小学1年生でも大部分の子供は
理解できるであろうというくらいです。
非常に簡単なものなので、考えているより実際にやってみたほうが、
よっぽど手っ取り早く理解してもらえると思います。

早速、目標としている図１の樹状図から円図を作ってみましょう。

まず、図１の樹状図で示されたのクモの形を折るために、円図を作るには
何個の円が必要が分からなくてはいけません。
円図に描かれる一個一個の円は、それぞれが、一個の折り出すカドに対応しています。
従って円図全体では、必要な円の数は、折り出したいカドの数と同じ数になります。
今、図１で示したように、折りたい目標形には、足に対応するカドが８個、
頭に対応するカドが１個、胴体に対応するカドが１個の合計１０個のカドがありますから、
必要な円の数も１０個となります。

さて、円が合計で１０個必要なことは分かりましたが、各円の半径は、
どのようにして決めればよいでしょうか？
これまた非常に簡単な話でして、
「折り出したいカドの長さと、そのカドに対応する円の半径は同じにすれば良い」のです。
たとえば、長さ１０ｃｍのカドを１個折り出すためには、
半径１０ｃｍの円が１個必要ということです。

ところで、いままで「折り出すカドに対応する円」を、単に「円」と書いてきましたが、
これからは、設計法の用語に従って「円領域」と呼ぶようにしましょう。 っていっても、円領域って実体は単なる円のことなので、
難しく考える必要は全然ありません。

さてさて、目標としている図１の形を折るためには、
どういう半径の円領域が何個づついるか考えてみましょう。

まず、前から一番目の足のカドは左右に１本づつで、合わせて２本あって、
長さは両方とも10ｃｍなので、
これに対応するには、半径10ｃｍの円領域が２個必要です。

さらに、前から二番目の足のカドは左右に１本づつで、合わせて２本あって、
長さは両方とも5ｃｍなので、
これに対応するには、半径5ｃｍの円領域が２個必要です。

さらに、さらに、前から三番目の足のカドは左右に１本づつで、合わせて２本あって、
長さは両方とも5ｃｍなので、
これに対応するには、半径5ｃｍの円領域が２個必要です。

さらに、さらに、さらに、前から四番目の足のカドは左右に１本づつで、合わせて２本あって、
長さは両方とも１０ｃｍなので、
これに対応するには、半径5ｃｍの円領域が２個必要です。

それから、頭のカドは、設計を柔軟に行うために、
カドの長さを可変長にして適当に変えられるようにしています。
したがって、このカドに対応する領域円は半径が可変で、
大きさがいろいろ変えられるものとします。

最後に、胴体のカドも、設計を柔軟に行うために、
カドの長さを可変長にして適当に変えられるようにしていますので、
このカドに対応する領域円も半径が可変で、大きさがいろいろ変えられるものとします。

以上、まとめますと、
図１の樹状図で示されたのクモの形を折るためには、
半径5ｃｍの円領域が４個、
半径10ｃｍの円領域が４個、
半径が自由に変えられる円領域が２個必要となります。


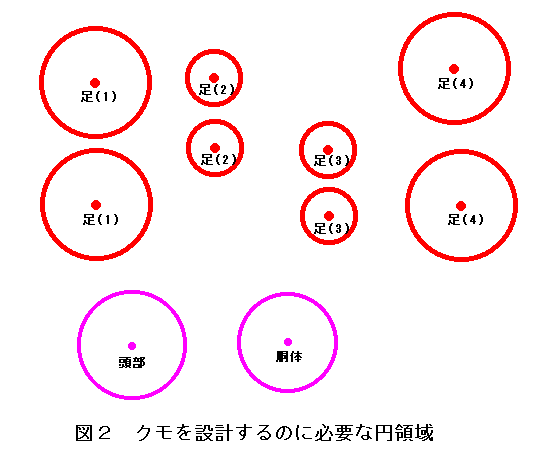
なには、ともあれこれらの円領域を描いてみましょう。図２をみてください。
ここでは円領域は赤で描くことにして、
各円領域が実際にはどのカドに対応しているかは円の中心付近に書き込むことにします。
特別に半径が可変長の円領域はピンク色で描く異にします。




ここまでの作業で、必要な円領域が全て揃いましたから、
今度はいよいよ円領域を正方形の用紙の中に効率良く詰め込みましょう。
でも、円領域を正方形に詰め込むといっても、初めてやる場合は、
どうすればいいか具体的にわからないと困りますよね。でも、ご安心ください。
円領域を正方形に詰め込む作業も、誰でも簡単に実行できる作業なのです。
これまた簡単な話なので、くどくど説明するより、実際に作業したほうが
分かりやすいので、早速実行しましょう。

実際に作業しようとして、なによりもまず気になることは、
「円領域を正方形に詰め込みするといっても、
正方形の大きさは一体どのくらいにするんだあああ？？？」ということかと思います。
しかし。案ずることはございません。正方形の大きさは適当に決めちゃえばよいのです。
ある大きさの正方形に円領域を詰め込みしていって、
「なんか狭そうだな」と思えば、正方形を大きくすればいいし、
「正方形が広すぎてスカスカだな」と思えば、正方形を小さくすればいいだけのはなしなのです。
というわけで、なんの不安もなく、適当な大きさの正方形に円領域を詰め込んでください。

ここである人は次のように思うかもしれません。
「だからー、適当な大きさの正方形に円領域を詰め込むったって、具体的にわからないってば」と。
この解答はいたってシンプルでして、「とにかく正方形に円を放り込む。それだけです。」
ということになります。
ただし以下の２つの「小学生でも理解できないやつはいない！」という条件は守ってください。
　条件その１：「どの円領域も、別の円領域と重なってはいけません」
　条件その２：「すべての円領域の中心は正方形の中にあること」
では、これらを満たすように円領域を正方形に詰め込んだ例を見てみましょう。
図３を見てください。図３にはいくつかの例が描かれていますが、全て正しい
「正方形への円領域の詰め込み例」です。


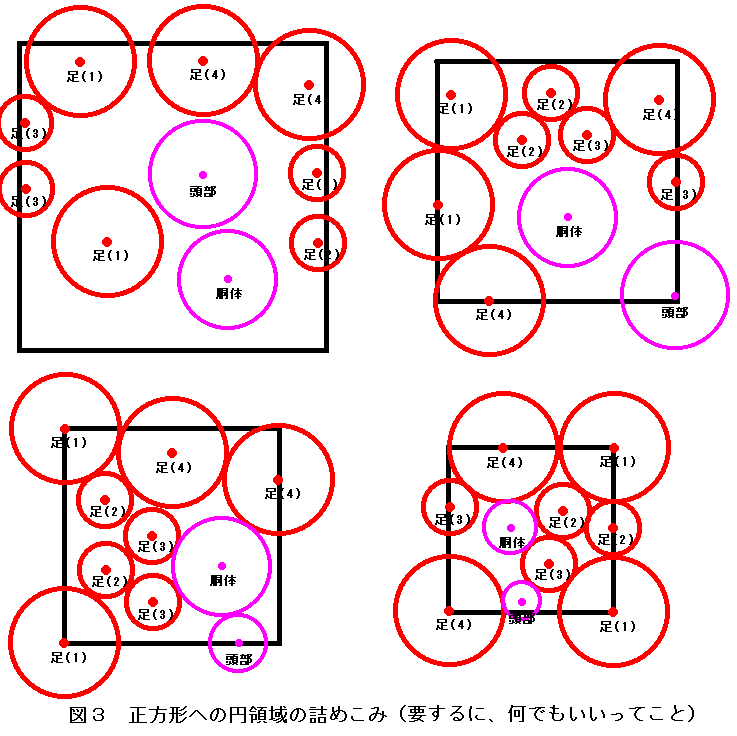
図３を見てもらえればすぐに気づいてもらえると思うのですが、
「正方形への円領域の詰め込み」をするときに守らなくてはいけない条件は、
めちゃくちゃ簡単な条件が、たったの２つだけしかないので、
当然ながら、正しい詰め込２パターンは１個だけではなく、無数にあります。
そこで問題になるのが、この無限のパターンから、いかにして良いパターンを
考え出して用いるかということです。
ここのところは、設計全体の作業の中でも大切なポイントです。
では、どういう「正方形への円領域の詰め込みパターン」が良いパターンなのでしょうか。
設計方法にあまり慣れてない人は、この辺で不安になってくるかもしれません。
しかし、心配することは全くありません。この判断も基本的な考え方は極めて単純なので
すぐに実際に使える判断ができるようになります。
ただし、ここは奥の深いところで、経験値が上がればあがるほど、
上手にいろいろな円領域の詰め込みパターンを使いこなす事ができるようになります。
しかし、別に最初から、うまくやろうとする必要は全くありませんのでご安心ください。
とりあえずこの文章を読んでいただければ、
１通りのパターンは使えるようになるはずです。
そして、その判断だけでも十分に多様な創作ができます。

さてココがポイントなのですが、クモは先述の様に、実は折紙のテーマとしては
相当難しいテーマに入ります。
本来なら「円領域の詰め込みパターン」はさまざまなパターンを自由に試してもらって、
その中から創作者が好みのパターンを選ぶのですが、こと、クモを創作する場合は、
自由に「円領域の詰め込みパターン」を試したら、かなり多くのパターンが
使い物にならない悲惨な結果におちいってしまうでしょう。
もちろん設計法自体に対して興味のある人が、それを承知の上で、
自由に「円領域の詰め込みパターン」を試してもらうのは大いに結構なのですが、
作品を創作することが目的の人は、そんな効率の悪いことはしたくないと思います。
そこで、クモを創作するときの設計上の重要なポイントを書いておきますので、
その点は留意しておいてください。
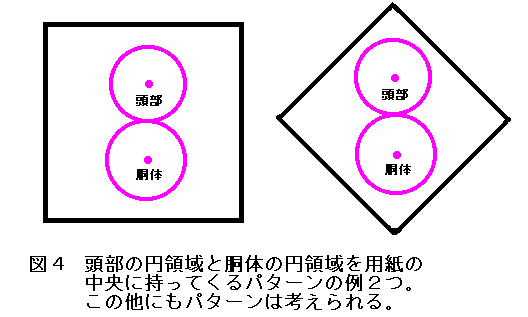
それは、図４のように、「頭の円領域と胴体の円領域はできるだけ正方形用紙の中央部に配置する」
ということです。「なんだ、そんなこと当然じゃん。」と思う人もいるかと思いますが
これは造形上重大な影響があるところで、さらに、
いろいろな盲点が重なっているところなので、決して軽視できないところなのです。


（注、詳しい方向けにちょっと解説、、、、内容がわからない方は読み飛ばしていただいて
結構です。
今年の夏に私は非対称クモを創作しました。この作品は従来のクモの折紙よりも
いくつかの点で造形上の利点を持っていました。その本質は足のカドの
非対称性もあるでしょうが、二つの円領域が用紙中央部に存在することのほうが重要
だと考えています。
さらに設計法上の解説をしますと、用紙辺部に足として必要な８個の円領域だけしか
配置していないことも重要な点です。設計法に詳しい方ほど、つい、折りやすいようにと、
用紙辺部左右対称線上に小さな円領域を追加したくなりますが、クモでは、こういう操作は
悪い影響を及ぼすこともあるようなので、これは慎重にすたいものです。）

さてさて、以上の予備知識を仕込んだ上で、いよいよ、良い「円領域の詰め込み」を
実現してみましょう。
そこで、「円領域の詰め込み」の良し悪しの大まかな判断基準を記しておきます。

　判断基準１：なるべく効率良く円領域が詰め込まれていること。
これは、いいかえると、正方形の大きさがなるべく小さい方がいいことと同じです。

　判断基準２；円領域の配置がなるべく、実物のパーツの配置と同じこと。
たとえば、１番目の足の隣に２番目の足が来てその次に３番目の足がくるというようなのが良いです。
これに対して、１番目の足の隣に４番目の足が来てその次に３番目の足がくるというようなのは
普通はまずいです。

基本はこの２つの判断基準だけでことたります。これまた簡単ですね。
（もっとも、おもしろい設計を行うためには、こういった常識的な判断基準にとらわれないことが
大事な場合もありますが、今回は手堅く、オーソドックスな方法でいきましょう。）
図５に実例をあげておきますので参考にしてください。
説明を考え込むよりは実例で雰囲気をつかんでもらったほうがとても簡単だと思います。






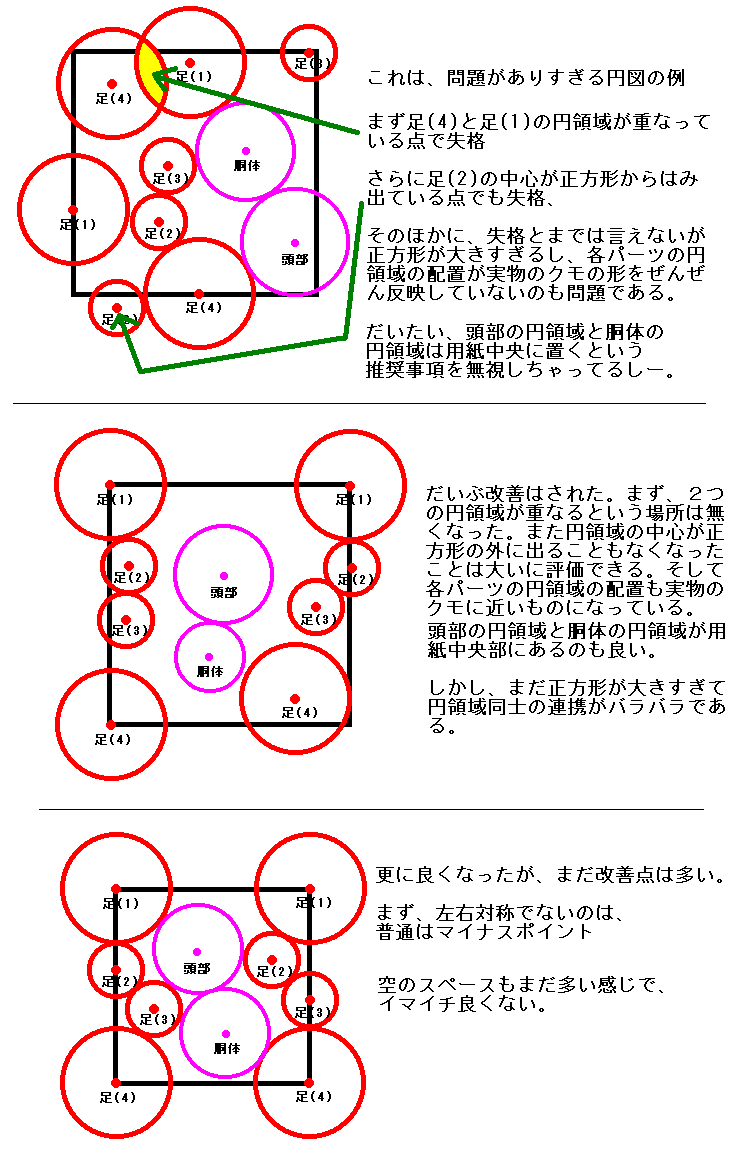
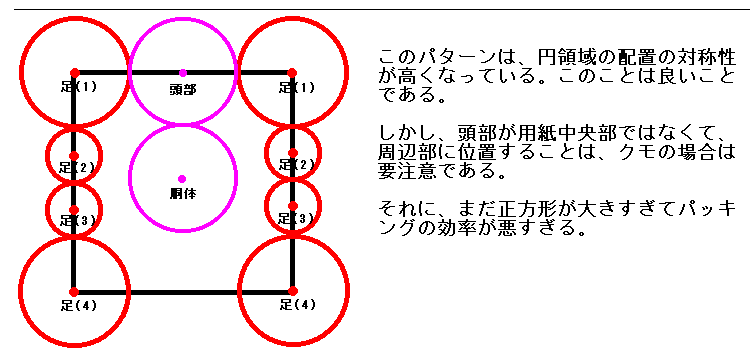
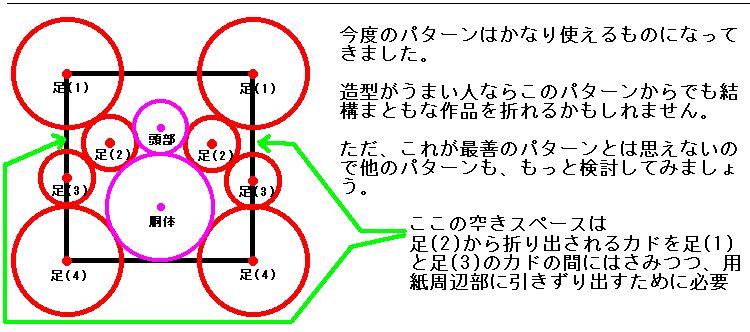
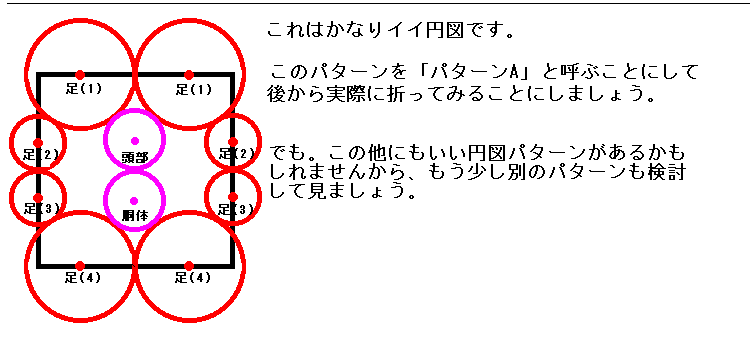
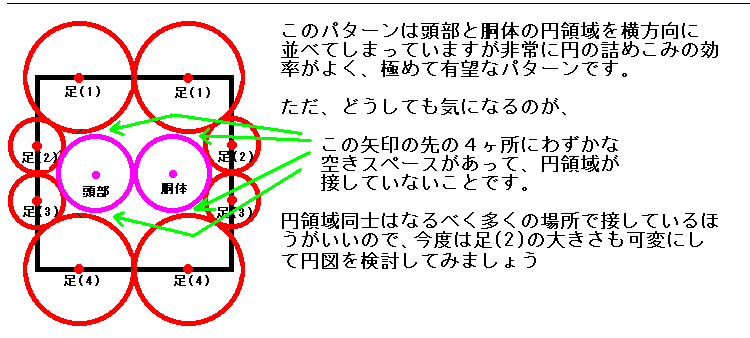
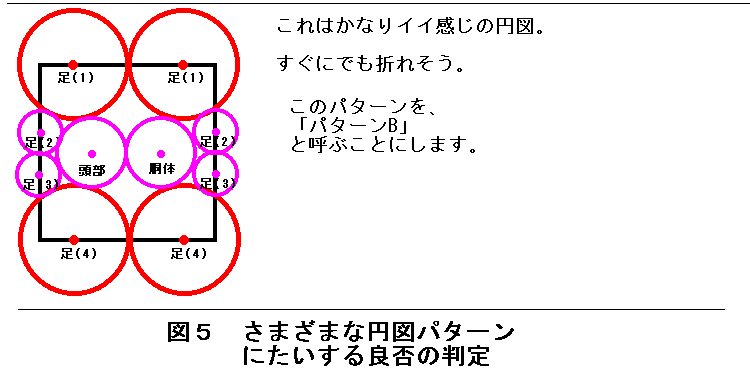
円領域の配置が決まって、円図が出来上がったら、設計の大まかな道筋がきまったと言ってもよいでしょう。
今回の図５の例では有望そうなパターンとして「パターンA」と「パターンB」の
２つをとりあえず作成ました。
どちらのパターンがイイのか実際に試してみないと分からないので、以後は、
この２パターンを並行させて検討していきましょう。


ただ、領域円の配置が決まったからといって、まだ実際の折り線までは分かっていませんから、
今度は、出来上がった円図を折りたたむことができるように、実際に折るための折り線を
円図に加えていくことにしましょう。
ここで具体的に、どうやって折り線をつけるかといういことはとりあえず置いといて、
円図全体の正方形を見渡して見ましょう。
次のようなことをなことを思った人は居ませんか？
「こんな、円がごちゃごちゃしてるところ全体に折り線をつけるなんて面倒くさいわ。
一度に全体に折り線をつけるより、円図を細かく分割して、その分割した部分ごとに折り線を
付けて、それを最後に再びまとめるほうが楽にきまってるだろ。」と。
この感覚は、ま、筋が通った感覚といえるでしょう。というわけで、折紙設計でも
実際に円図を細かく分割して、分割した部分ごとに折り線を付けて行くと言うのが
まあ、一般的な折紙設計のやり方なのです。
で、この分割するときに出てくるのが、折紙分子というものです。
要するに、円図（展開図）の全体なんて面倒くさくて考えていられないので、円図（展開図）を
折紙分子に分けて、
その分割された分子の中の折り線だけを、各分子ごとにつけていこうと
言うわけです。
こう説明しますと、心配性の人は次のように考えるかもしれません。
「本当に分子なんて物に分けて考えても良いものだろうか。
一つ一つの分子に分けて折り線を付けた段階では、うまく折れても、
全分子を再統合して全体で折ったときは隣り合った分子同士で折り線が合わなくなって
破綻することはないのだろうか。」と。うーん、もっともな疑問ではあるのですが、この答えは
きわめて簡単です。円図を、決められた規則を満たすようにして分子に分割して、次に、
各分子に、ある条件を満たすようにして折り線を付けたものは、
絶対に、必ず、何があっても、折りたたむことができるのです。
というわけで、円図ができたら、それは分子に分割してください（非常に簡単な手続きでできます）。
分子に分割したら、各分子は、決められた条件（これまた、きわめて簡単な条件なのですが）
を満たしてさえいれば自由に折り線をつけられます。そうして各分子に折り線を付けたものを、
まとめ合わせた全展開図は、必ず、絶対、何がなんでも折りたたむことができるのです。
（実は分子内部に折り線を付けるという操作は、設計者が自由変更できる操作ですので、
各創作者の技術の差が現われてくるところです。
といっても心配することは全くありません。とりあえず折れるようにするだけなら極めて簡単で、
すぐできるようになりますし、それだけでも結構見れるものになることも多いものです。
なお、ここは詳しく言うと,「展開図の洗練化」という操作とも重なっているところです）。

円図を分子に分割し折り線まで付けるところまでやってしまえば、とりあえず実際に折れる展開図が
設計できたことになるのです。
さあ、だんだんゴールが見えてきました。もう一息です。がんばりましょう。

では、実際に円図を分子に分割してみましょう。なお、ここでは一値分子というものが
最も簡単で使いやすい分子ですので、それを使うように操作を進めていきましょう。

では、実際にどうやって円図を分子に分割するかですが、これを行うためには、
一値分子というものの実態を知っている必要なんて全くありません
（もちろん知っているにこしたことはありませんが、、、）。
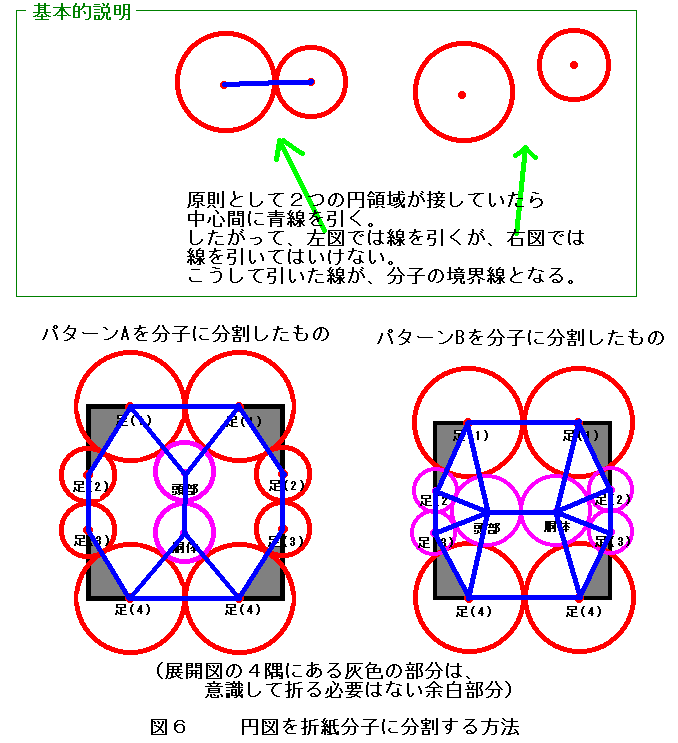
全く何の予備知識も要らない、単純な操作なので、とりあえず図６で説明していることを読まれて、
皆さんも何も悩まずに実行してください。
要するに、やることは、
「2個の円領域が互いに接している場合、両方の円領域の中心を結ぶ直線を引くこと」
だけです。それ以外の操作は一切必要ありません。
すべての接している円領域同士をチェックして、それらの中心間にもれなく線を引いてください。
（ここでは線の色は青で引くことにします）。

さて、円図が分子まで分割できたら、次は、いよいよ各分子の内部に実際に折るための
折り線を付けましょう。
さて次のように思った方はいませんか？「円図全体だったら、最初の樹状図のように
折ることを目標にしていたわけだけど、分子に分割しちゃったら、
各分子はどういう形になることを目標にして折ったら良いのかわからんわい。」と。
でも心配は無用です。大体、全体の円図を分割して分子にしたのだから、
各分子を折った形は、全体の円図を折った樹状図の形より簡単になっているに
決まってるいますしね。
といっても、実際に各分子がどういう形になることを目指して折り線を付けていったら
良いのか分からないと困っちゃうかもしれません。でもそれは、簡単にわかることなのです。
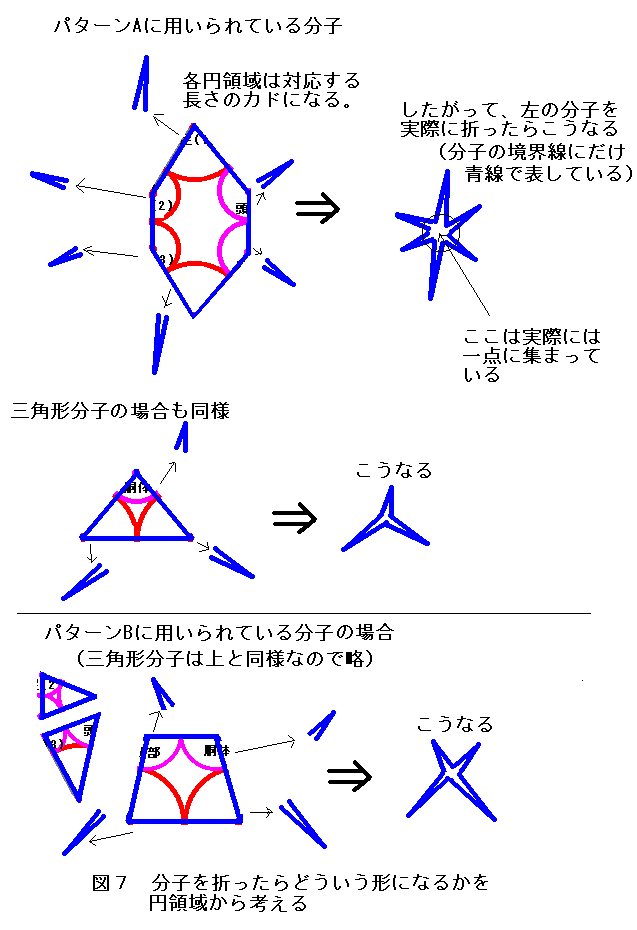
どうやったら分かるかというと、そもそも各分子の境界線にそって、円領域が並んでいるのですから、
この円領域が、それぞれ対応するカドになるように折ればいいだけのことなのです。
具体的な例を図７で示してみます。

さてここで、物覚えのいい方は、あることが気になっておられるのではないでしょうか。
「一値分子についての説明がぜんぜんないんだけど、いったい、一値分子の一値性っ何なの？」と
えっとですね、実は一値性って、忘れていたなら、忘れたままでも別にかまわないのですけど、
簡単に覚えられて、かなり便利なのもなので、とりあえず覚えておきましょう。
一値性とは、分子を実際に折ったときに、その分子の境界線がすべて一直線上に集まる性質のことです。
この一値性を持った分子のことを一値分子といいます。
一値性の説明には以下のリンク先にありますので、いっしょに読んでおいてください。
一値性とは

先ほど、「各分子の内部に折り線を付けるには、分子の境界線にそって並んでいる円領域が、
対応する長さのカドになるように折っていく」と書きましたが、そのときに、
同時に一値性も満たすようにして欲しいのです。
ある人は次のように思うかも知れません。
「一値性なんてイチイチ意識して折るなんて、わずらわしいわい」と。
ところが、実際には一値性を意識したほうが折りの目標が限定されてくる分、かえって
折りやすく感じるたりするものです。そういうわけで、是非は一値性は活用してもらいたいと思います。
では、実際に一値分子として各分子に折り線を付けてみましょう。
まずは、最も簡単な三角形分子に折り線を付けてみます。
これには「内心の定理」というものを使って折り線を付ければいいのですが、（これも簡単な操作です）
それについては以下のページに例がありますので、
今回のクモ折紙の「パターンA」や「パターンB」の中に含まれている三角形分子はその説明のようにして折ってください。
内心の定理を体感しよう
さて、三角形分子は簡単に一値分子として折り線がつけられますが、
その他の多角形分子を一値分子として折るにはどうすればイイでしょうか。
色々な方法はあるのですが、結局は各人が適当に折って、一値分子の条件（各境界線が一直線上に乗る）
ことさえ満たされていれば何でもいいわけですから、
要するに、「各自適当に折ったらそれでよし」というのが最も実情を反映していると
思います。
そうはいっても、具体的な折り方の例も見てみたい人も居るでしょうから、
図８で実際に多角形分子に折り線を付けてみます。




すべての分子に一値分子としての折り線を付け終わったら設計は終了です。
こうしてできた展開図は必ず、絶対、どんなことがあっても折り畳み可能ですから
安心して折ってください。
ここで大事なことは
************************************************************************
ここをクリックすると、メインページに戻ります。