ここをクリックすると、メインページに戻ります。
===============================================================================
=====第４話　内心の定理を体感しよう======

折紙の展開図を合理的に解釈しようという試みにはさまざまなものがあります。
内山興正氏の「折り紙」（1962年、国土社）や「純粋折り紙」（1979、国土社）や
前川氏の「ビバ折り紙」などのはご存知のかたも多いと思います。
そしてまた、伏見夫妻による「折り紙の幾何学」（1979、日本評論社）も折紙の
合理的な考え方の発展に大きな影響を与えた本といえるでしょう。
この中で現代の折紙設計における極めて重要な定理がいくつか発表されました。
そのひとつに内心の定理というものがあります。内心などど聞くと、中学校時代の
数学の時間を思い出しますが、折り紙の内心の定理は、学校の授業でうけた
印象より、ずっと簡単に体感できるようものです。そして、この定理は折紙設計の
基本技法として最も使いでのあるものの一つです。ぜひとも、ここで、その簡単さを体得して
みてください。

早速その定義を見てみましょう
折紙設計における内心の定理とは、
「適当な形の三角形を、その３つの頂角の二等分線で折ると
三角形の３つの辺が一値性を持ちながら平面に折りたたむことができる。」
というものです。このとき３つの頂角の二等分線は三角形の内心で交わるので
内心の定理というわけですが、あまり細かいことは考えたくないという人は、
そういったことは、無視してもかまいません。ぶっちゃた話、実用的に大事なことは
「適当な三角形は、各頂角の二等分線で折ると、うまくおれるんだあぁぁぁぁ!!!」
ということだけです。とりあえずそだけは押さえてください。（いろいろと細かいことを
考えるのも面白いところなので、好きなかたはその意味を良く考えてもらいたいと
思います。）

さて、では実際に適当な三角形を、内心の定理で折って見ましょう。
このとき、適当な三角形は一値分子となっていることを忘れないでください。
図１がその様子です。実際にいろいろな形の三角形で試してみてもらえば、
この定理が、すごく素直なものであることがわかってもらえると思います。


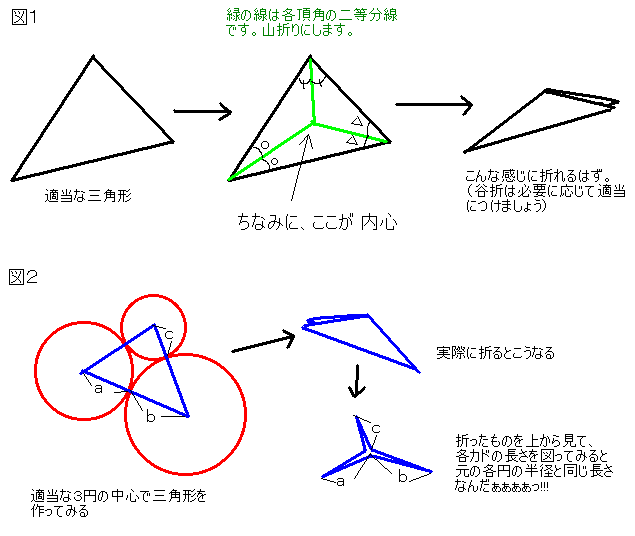
次に、図２のように、適当な大きさの３つの円を、各円が接するように描いて
その中心を結んで三角形を作ってみましょう。
この三角形をやっぱり内心の定理で折ってみると、どうなるでしょう。
この三角形を折ったものの３つのカドの大きさ（長さ）に注目して
もらいたいのです。それぞれの長さが、もとの円の半径とまったく同じになっている
のです。
これこそが、折紙設計において、「折り出したいカドを円で表して設計できる」
ということの基本原理なのです。

なお、この第４話や、第５話の話は「詰め折り紙」コーナーや
「折紙設計のあんなことやこんなこと」コーナーと関連していますので、
以下にリンクを張っておきましたので、余裕のある方はあわせて読んで見てください。

「詰め折紙」コーナー
基本編.第１問
「折紙設計のあんなことやこんなこと」コーナー
円図から展開図をかく.....一見複雑そうでも、基本はこの第４話と同じです。
一値分子の内部に折り線をつける


************************************************************************
ここをクリックすると、メインページに戻ります。