ここをクリックすると、メインページに戻ります。
===============================================================================
=====第５話　４個の円を組み合わせてみよう======

この前の第４話の内心の定理の項で、「３つの円を接するように配置したとき、
接する円どうしの中心を直線で結んでできた三角形は、もとの各円の半径と全く
同じ長さのカドを持つように折り畳むことができる」ということを見てみました。
さて、３つの円でそういうことができるのなら、４つの円でも同じようなことが
できるのだろうかという疑問がわき上がってきます。
答えを先に書いてしまうと「４円でもできるけれども注意を要する」ということになります。
注意を要するって一体なんだろうと思われるかもしれませんが、そんなに面倒な
ことではありません。ちょっと話がもどりますが、３円の場合は、それによって
できた三角形を、各頂角の二等分線を折り線として、自然に折ると、目的（円の
半径と同じ長さのカドを折ること）が達成できたのですが、４円の場合は、それに
よってできた四角形を、各頂角の二等分線を折り線として、自然に折っただけでは
もとの各円の半径と、折りあがったカドの長さとが通常は一致しないことが多いのです。
この辺の事情は図１を見てください。


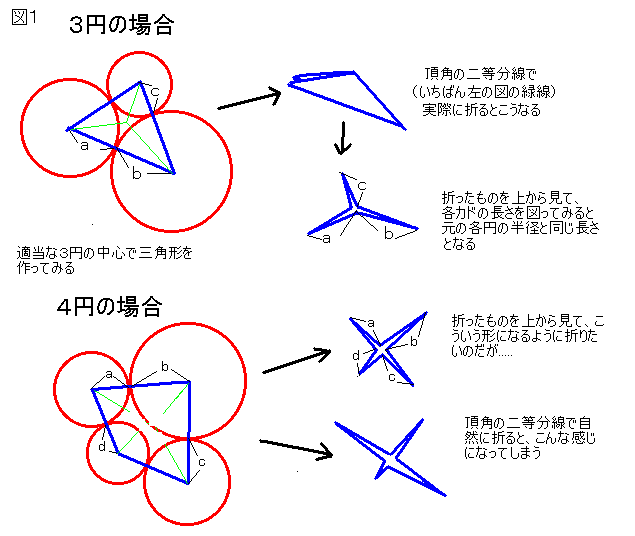
「うーん、じゃあしょうがないなあ、４円を接して作った四角形を、もとの円の
半径どおりに折ることはやめとこっかー」などと諦めないでください。４円からなる
四角形をもとの円の半径どおりに折ることは、ちょっとやそっとでは諦められない
非常に重要な特別の意味を持っているのです。それは何かと言いますと、「もっと
多くの円（例えば７個の円とか１５個の円でも）が接するようして作った多角形
（例えば７角形とか１５角形でも）は適切に円を加えることによってどんな場合でも
３円からなる三角形と４円からなる四角形の集合体に分割できるのです（図２を参照）。


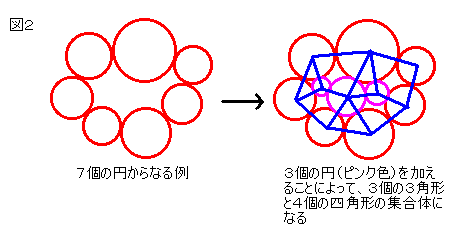
今、３円からなる三角形をもとの円の半径に対応して折れることはすでにわかって
いますから、もし、更に４円からなる四角形をもとの円の半径に対応して折れる
ことができるのならば、このことは、どんなに多数の円による多角形でも、もとの
円の半径とカドの長さを同じにして折り畳むことができるということ意味しているのです。
要するに、多数のカドを折りだす場合は、いちいち７個の円の場合とか１５個の円の
場合とかを分けて考える必要はなくて、３円からなる場合と４円からなる場合を
組み合わせれば、いくらでも多数のカドが折り出せることになるのです。そういうわけで
４円からなる四角形を、もとの円の半径どおりに折ることは、ちょっとやそっとでは
諦められない訳です。では、４円からできた四角形を円の半径に応じて折るには
どうすれば良いのでしょう。
その方法は、実はたくさん在ります。一値性に注意して適当に折っていれば結構
折れちゃって、それで十分なのですが、一応こうすれば絶対折れるという折り方の
一つに加円法というのがありますので、その手順を見てみましょう。
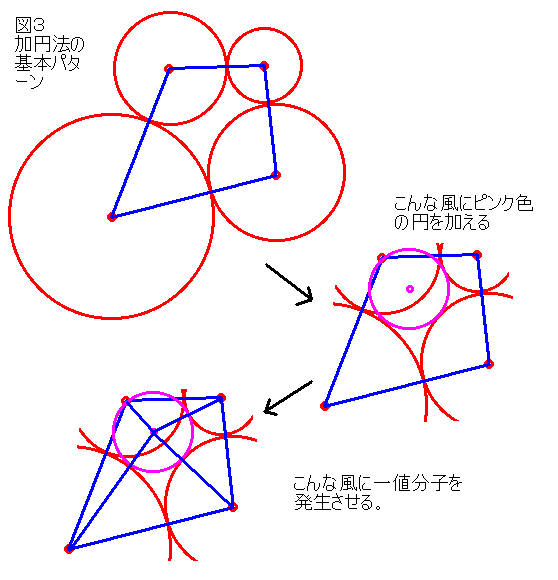
この方法は新たに円を加えることによって、４個の円領域の内部の空間を埋めて、
一値分子に分割する折り線を求める方法です。図３に加円法の基本パターンを
示しておきますのでご覧ください。

なお、加円法に関しては後からもう少し詳しい話を追加したいと思います。
------------------------------------

なお、この第５話や、先の第４話の話は「詰め折り紙」コーナーや
「折紙設計のあんなことやこんなこと」コーナーと関連していますので、
以下のリンク先を、興味のある方はあわせて読んでみてください。

「詰め折紙」コーナー
基本編.第１問
「折紙設計のあんなことやこんなこと」コーナー
円図から展開図をかく.....一見複雑そうでも、基本はこの第４話と同じです。
一値分子の内部に折り線をつける


************************************************************************
ここをクリックすると、メインページに戻ります。